\newcommand{\lpf}{\textnormal{lpf}} \newcommand{\eps}{\varepsilon} 之前做 PE 的时候看到一个很有用的数论技巧：令 $\lpf(x)$ 表示 $x$ 的最大质因数，我们考虑把 $[n]$ 分成按照 $\frac{x}{\lpf(x)}$ 来分类，即 $S_k = \{x: x / \lpf(x) = k\}$，然后每一个 $S_t$ 单独处理。举个例子，假设我们要求一个积性函数 $f$ 的前缀和 $F(x) := \sum\limits_{n=1}^x f(n)$，那么对于一个 $S_k$，它里面的数的函数和为：

$$\sum_{n \leq x: n / \lpf(n) = k} f(n) = f(k \lpf(k)) + \sum_{\lpf(k) < p \leq x / k} f(kp) = f(k \lpf(k)) + f(k) \sum_{\lpf(k) < p \leq x / k} f(p).$$

后者只要知道形如 $\tilde F(x) := \sum\limits_{p \leq x} f(p)$ 这样的和就可以了，而这个是有经典解法的。这个算法的更详细的介绍请参考 The prefix-sum of multiplicative function: the black algorithm 和 关于一种积性函数前缀和的通用筛法的时间复杂度证明 - 知乎。

显然，这个算法的整体复杂度取决于 $\tilde F$ 的计算复杂度和有多少个不同的 $k$。由于每个问题的 $f$ 性质不同，$\tilde F$ 的复杂度会有不同，但是后者相对独立。这里我们就开始研究有多少个不同的 $k$，即 $Q_x := \#\{n / \lpf(n): n \leq x\} = \#\{k: k \lpf(k) \leq x\}$ 的大小。

遇到这种不会做的题，第一反应是打个表：这里我就直接用了 baihacker 的结果了：

1e5     1.89e+03                    1894        0:00:00:00.000
1e6     9.11e+03                    9108        0:00:00:00.000
1e7     4.49e+04                   44948        0:00:00:00.000
1e8     2.28e+05                  228102        0:00:00:00.000
1e9     1.19e+06                 1185818        0:00:00:00.001
1e10    6.30e+06                 6298637        0:00:00:00.006
1e11    3.41e+07                34113193        0:00:00:00.036
1e12    1.88e+08               188014195        0:00:00:00.222
1e13    1.05e+09              1052806860        0:00:00:01.194
1e14    5.98e+09              5981038282        0:00:00:06.885
1e15    3.44e+10             34430179518        0:00:00:39.958
1e16    2.01e+11            200620098564        0:00:03:52.337

之后怎么办？当然是查万能的 OEIS 啦！可惜的是，OEIS 上并没有这类序列。我们再回去看之前那篇知乎文章。它里面的定理 11 用这里的语言可以表述为：

对于任意常数 $\alpha < 1$，我们有 $Q_x = \Omega(x^\alpha)$.

……似乎陷入僵局。但是我们再看看 baihacker 的表，这数字也差的太多了吧……也就是说，$\Omega(x^\alpha)$ 里的常数取决于 $\alpha$，但是随着 $\alpha$ 的增加，这个常数可以非常小，例如当 $n = 10^{16}, \alpha = 0.99$ 时，藏在 $\Omega(n^\alpha)$ 里的常数最大也不过 2.9e-5，在这个 $n$ 的范围上都不能看成是常数了……于是我就想能不能搞一个紧一点的 bound，而且最好是一个上界，因为我更关心这个算法实际中有多快。

然后开始查文献……令 $\Psi(x, y)$ 表示 $[x]$ 中有多少个最大质因子不超过 $y$ 的数。我们能得到一个 trivial bound：

$$Q_x \leq \frac{x}{y} + \Psi(x, y).$$

剩下的问题就是怎么 bound $\Psi(x, y)$ 以及取一个合适的 $y$ 了。

这里有一篇 survey Integers without large prime factors 来讲怎么 bound $\Psi(x, y)$ 的，其中提到 A. Hildebrand 在 On the number of positive integers <= x and free of prime factors > y 里给出了某个范围内最好的估计：

对于任何常数 $\eps$，且 $x \geq 3, 1 \leq u \leq \log x / (\log \log x)^{5/3 + \eps}$，有

$$\Psi(x, x^{1/u}) = x \rho(u) \left( 1 + O_\eps\left( \frac{u \log (u + 1)}{\log x} \right) \right),$$

其中 $\rho(u) = \exp(-(1 + o(1))u \log u)$ 为 Dickman 函数。

带入回之前的 bound，有：

$$Q_x \leq x / x^{1/u} + \Psi(x, x^{1/u}) = x \exp\left(- u^{-1}\log x \right) + x \exp(-(1 + o(1)) u\log u).$$

聪明的同学可以看出来，这里取 $u = \sqrt{2 \log x / \log \log x}$ 就有：

$$Q_x \leq x \exp\left( - (1 + o(1)) \sqrt{2 \log x \log \log x} \right).$$

---

本来故事到这里就差不多结束了，但是我突然灵机一动，转换了一下思路。聪明的同学已经发现了，如果 $Q_x \neq Q_{x - 1}$，那么就意味着 $\lpf(x)^2 | x$。于是我们就把所有满足 $\lpf(x)^2 | x$ 的数列出来，看这个序列的增长速度就可以了：

$$4, 8, 9, 16, 18, 25, 27, 32, \dots$$

这个序列我们就能在 OEIS 上找到了，为 A070003 - OEIS，上面还提到 Erdos 证明了

$$Q_x = x \exp\left(-\left(1 + o(1) \right)\sqrt{\log x \log \log x} \right).$$

好了，直接撞人家枪口上了，比我小一个常数 $\sqrt{2}$……我去看了一下论文 On products of factorials，里面只轻飘飘提到一句：

An old result of one of the authors states that the number of bad’ $n < x$ is

$$x e^{-(1 + o(1)) (\log x \log \log x)^{1/2}}.$$

怎么连引用了哪篇都不说……

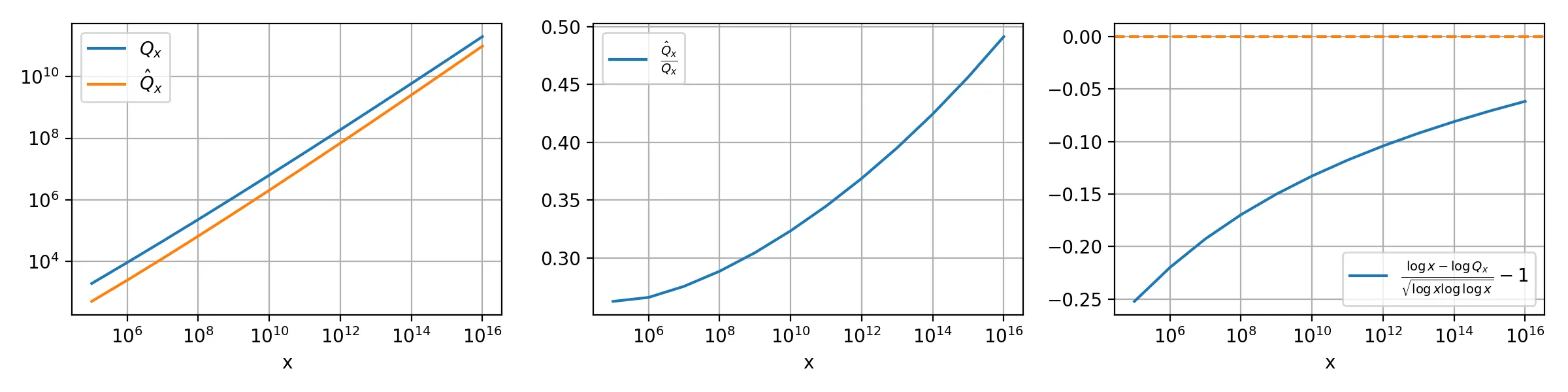
我试了一下，这个 bound 其实挺紧的：我们画出了 $Q_x$ 和 $\hat Q_x = x \exp(- \sqrt{\log x \log \log x})$，两者之间的比例，以及 $(\log x - \log Q_x) / {\sqrt{\log x \log \log x}} - 1$：（代码）

---

我在查文献 On sums involving reciprocals of the largest prime factor of an integer 的时候还看到这么一个有趣的结果：

$$\sum_{n \leq x} 1 / \lpf(n) = x \exp\left( -\sqrt{2 \log x \log \log x} + O\left(\sqrt{\log x \log \log \log x} \right) \right).$$

聪明的同学已经看出来了，这和我们估计的 $Q_x$ 一模一样啊……事实上，我们想要的就是

$$Q_x = \sum_p \Psi(x/p^2, p) \leq \sum_{p} p^{-1} \Psi(x / p, p),$$

所以得到类似的结果也不奇怪 →_→ 我稍微看了一下其证明思路，感觉可以用来证明 Erdos 的那个更紧的 bound，大概就是：

$$\sum_{n \leq x} 1 / \lpf(n) = 1 + \sum_{p} p^{-1} \Psi(x/p, p),$$

然后也去 bound $\Psi(x / p, p)$。

顺便一提，Erdos 1929-1989 内所有的 paper 都在 renyi.hu/~p_erdos/Erdos.html，各位有兴趣可以读读 →_→ 以及还有一篇更新的关于 $\Psi(x, y)$ 的 survey Integers without large prime factors: from Ramanujan to de Bruijn。