现在不是刚好在高考嘛,我也来看了一下,看有没有新东西……

下界
显然,我们只需要关注下标就可以了。直接搞第三问吧……
先来一张图证明:对于任意 0≤i≤j≤m,{1,…,4m+2} 是 (4i+1,4j+2) 可分的。图里同样背景颜色的数字在同一组,黑色表示删去的两项。
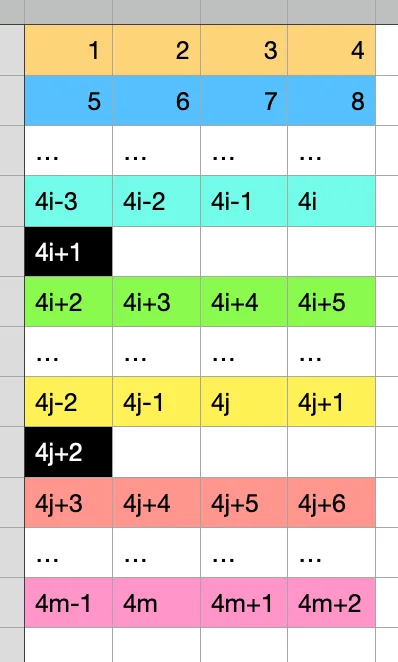
再来一张图证明:对于任意 0≤i<m,0≤j≤m 且 i+1<j,{1,…,4m+2} 是 (4i+2,4j+1) 可分的:
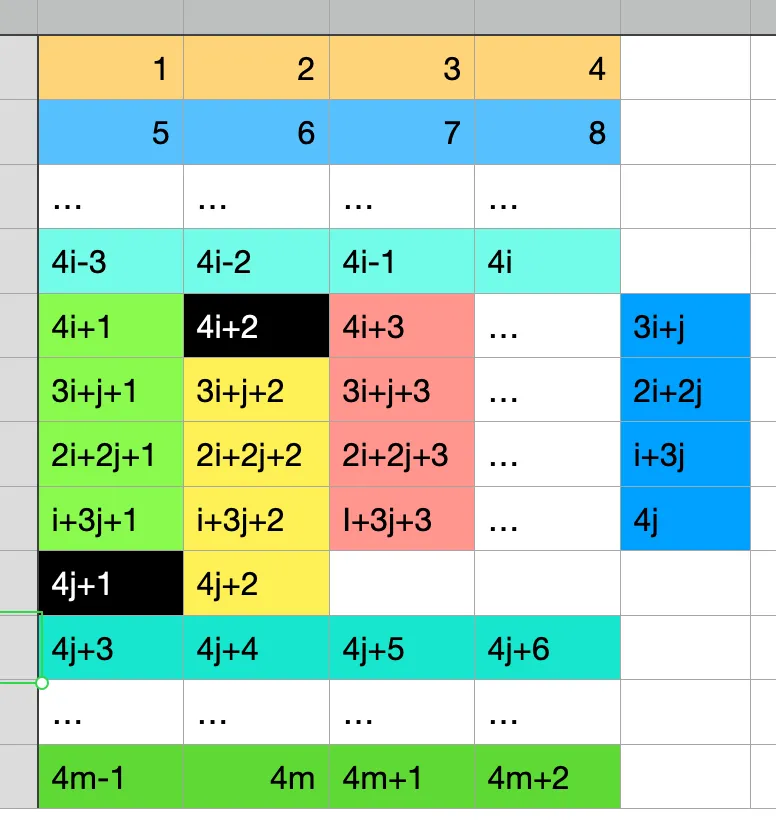
只算这两种情况,我们可以得到 Pm 的一个下界:
Pm≥(24m+2)(2m+2)+(2m)=8m2+6m+1m2+m+1>81.
证毕。
上界
既然我们都有下界了,那我们也不妨来算算上界吧。这里我们直接给出结论:刚才分析的两种情况几乎就是全部可分的情况了:
8m2+6m+1m2+m+1≤Pm≤8m2+6m+1m2+2m+1.
下面给出证明。
假设 (i,j) 可分,我们来推测 (i,j) 的性质。令 S∗={1,…,4m+2}. 我们来证明 (i,j) 必然一个 mod 4 = 1,另一个 mod 4 = 2.
证明
令 g(A)=∑i∈Aωi,其中 ω=i 为四次单位根,则对于任何一个长为 4 的等差序列 A={u,u+v,u+2v,u+3v},均有
g(A)=ωu(1+ωv+ω2v+ω3v)=0.
又有
g(S∗)=1≤i≤4m+2∑ωi=ω+ω2=i−1.
所以删掉的两个数 (p,q) 必须满足 ωp+ωq=i−1,证毕。
之前用了一个非常啰嗦的证明……
对于任何序列 S,令 f(S)i 表示该序列中 ≡i(mod4) 的数目。易得
f(S∗)=[m,m+1,m+1,m],
我们先观察长度为 4 的等差数列 A={u,u+v,u+2v,u+3v},对公差 v 分类后可以得到 f(A) 的所有可能性:
- v≡0(mod4):[4,0,0,0],[0,4,0,0],[0,0,4,0],[0,0,0,4];
- v≡1,3(mod4):[1,1,1,1];
- v≡2(mod3):[0,2,0,2],[2,0,2,0]。
通过逐步观察,我们可以确定 {imod4,jmod4}:
- 任何情况下,f(A)0+f(A)1≡0(mod2),而 f(S∗)0+f(S∗)1≡1(mod2),故 i,j 中有恰好一个数 ≡0,1(mod4) ,另一个数 ≡2,3(mod4)。
- 任何情况下,f(A)0+f(A)2≡0(mod2),而 f(S∗)0+f(S∗)2≡1(mod2),故 i,j 中有恰好一个数 ≡0,2(mod4) ,另一个数 ≡1,3(mod4)。
- 故 {imod4,jmod4} 只能是 {0,3} 或 {1,2}。
- 任何情况下,f(A)1−f(A)3≡0(mod4),而 f(S∗)1−f(S∗)3≡1(mod4),故 {imod4,jmod4} 只能为 {1,2}。
聪明的同学已经看出来了,这里就是在 Z44 下试图用 f(A) 的线性组合来表达 f(S∗)−f({i,j})。
显然,所有可能的 (i,j) 对的数目就是 f(S∗)1f(S∗)2=(m+1)2。这样就证明了我们的上界。
容易观察到,这里的上界和下界只差一种情况:就是 i≡2(mod4),j=i+3 这种情况。我感觉这种情况应该是不合法的,但是我证不出来了……


